Questão 15 - 1º dia - Segunda fase - Unicamp 2012
Oferecimento:
O número áureo é uma constante real irracional, definida como a raiz positiva da equação quadrática obtida a partir de
.jpg)
a) Reescreva a equação acima como uma equação quadrática e determine o número áureo.
b) A sequência 1, 1, 2, 3, 5, 8, 13, 21, ... é conhecida como sequência de Fibonacci, cujo n-ésimo termo é definido recursivamente pela fórmula
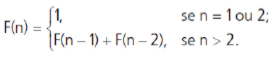
Podemos aproximar o número áureo, dividindo um termo da sequência de Fibonacci pelo termo anterior. Calcule o 10º e o 11º termos dessa sequência e use-os para obter uma aproximação com uma casa decimal para o número áureo.
Respostas
a) Resolvend a equação
.jpg)
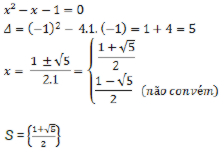
b) Da sequência dada, segue:
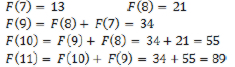
Então, a aproximação pedida é dada por:
a)
b) 1,6


