O conteúdo de frações é vasto e, por isso, aparece com frequência em questões do Enem. Entretanto, é mais comum encontrá-lo no desenvolvimento da resolução das questões do que exercícios propriamente direcionados a elas. Sendo assim, discutiremos cada operação matemática básica envolvendo frações e o modo de realizá-la para posteriormente discutirmos alguns exemplos resolvidos e comentados de questões do Enem envolvendo frações.
Frações são números que pertencem ao conjunto dos racionais e representam uma parte de algum objeto que foi dividido igualmente. Sendo assim, as frações representam os seguintes números: decimais finitos, dízimas periódicas e inteiros. Assim, todas as operações e propriedades válidas para esses números também são válidas para as frações.
As frações são representadas da seguinte maneira: dados os números inteiros a e b, com b diferente de zero, temos:
a
b
Essa é uma fração que representa a divisão de a por b. Nela, a é chamado de numerador e b é chamado de denominador.
Multiplicação de frações
Para multiplicar duas frações, multiplique numerador por numerador e denominador por denominador. Observe o exemplo:
10 · 15 = 10·15 = 150
12 20 12·20 240
Divisão de frações
A divisão de frações é feita por meio de uma multiplicação exatamente como no caso anterior. Porém, antes de multiplicar, é necessário inverter a segunda fração. Assim, é possível concluir que a divisão é igual a uma multiplicação por inverso. Observe:
2 : 3 = 2 · 5 = 2·5 = 10
6 5 6 3 6·3 18
Adição e subtração de frações
As duas operações são feitas da mesma maneira, com a única diferença de que, na adição, os números são somados e, na subtração, são subtraídos. Para isso, existem dois casos:
1º caso: Quando os denominadores das frações são iguais
Quando as frações a serem somadas ou subtraídas possuem denominadores iguais, a operação resume-se a somar ou subtrair os numeradores. Nesse caso, o denominador igual deve ser apenas repetido no resultado. Confira:
14 – 24 = 14 – 10 = – 10
21 21 21 21
Observe que o sinal do resultado ficou negativo por causa da regras dos sinais.
2º caso: Quando os denominadores são diferentes
Quando os denominadores são diferentes, não é possível somar as frações. Entretanto, existem frações diferentes que representam o mesmo número: as chamadas frações equivalentes. Se for possível encontrar frações equivalentes às frações dadas com denominadores iguais, basta somá-las como no primeiro caso. Veja um exemplo:
1 + 3
2 4
Observe que os denominadores são diferentes, mas a fração 1/2 é equivalente a 2/4, pois ambas representam o número 0,5. Portanto, a soma acima terá o mesmo resultado que a soma abaixo:
2 + 3
4 4
Resolvendo:
2 + 3 = 2 + 3 = 5
4 4 4 4
Para comprovar isso, faremos as contas usando os números decimais que cada fração representa: 1/2 = 0,5 e 3/4 = 0,75. Observe que 0,5 + 0,75 = 1,25. Dividindo 5 por 4, teremos: 5/4 = 1,25.
Note que os resultados apenas foram escritos de formas diferentes, mas tanto a fração quanto o número decimal são o mesmo número.
Método prático
Existe um método prático para encontrar frações equivalente em uma adição ou subtração de frações:
1 – Faça o mínimo múltiplo comum dos denominadores;
2 – Encontre frações equivalentes às frações dadas com denominador igual ao mínimo encontrado;
3 – Faça a adição ou subtração.
Para resolver a subtração abaixo, por exemplo, faremos o seguinte:
3 – 5
12 15
Passo 1:
12, 15| 2
6, 15 | 2
3, 15 | 3
1, 5 | 5
1, 1 | 60
Passo 2: precisamos encontrar uma fração equivalente a 3/12 com denominador igual a 60 e uma fração equivalente a 5/15 com denominador igual a 60. Para tanto, escreva o seguinte:
–
60 60
Para completar as lacunas, divida o denominador 60 da primeira fração do resultado pelo denominador 12 da primeira fração dada no exercício e multiplique o resultado pelo seu numerador.
60:12 = 5
5·3 = 15
Esse resultado é o numerador da primeira fração. Para encontrar o numerador da segunda fração, repita o procedimento:
60:15 = 4
4·5 = 20
Então, as frações que serão subtraídas são:
15 – 20 = 15 – 20 = – 5
60 60 60 60
Potenciação de frações
A potenciação de frações é uma extensão da multiplicação de frações, pois potências são produtos em que os fatores são iguais. Sendo assim, eleve à potência o numerador e, depois, o denominador. Observe o exemplo:
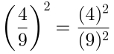
Radiciação de frações
A radiciação de frações também deve ser feita separadamente para numerador e para denominador de acordo com as propriedades da radiciação em cada caso e se necessário. Observe o exemplo:
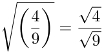
Exemplos
(Enem 2015) O polímero de PET (Politereftalato de Etileno) é um dos plásticos mais reciclados em todo o mundo devido à sua extensa gama de aplicações, entre elas, fibras têxteis, tapetes, embalagens, filmes e cordas. Os gráficos mostram o destino do PET reciclado no Brasil, sendo que, no ano de 2010, o total de PET reciclado foi de 282 kton (quilotoneladas).
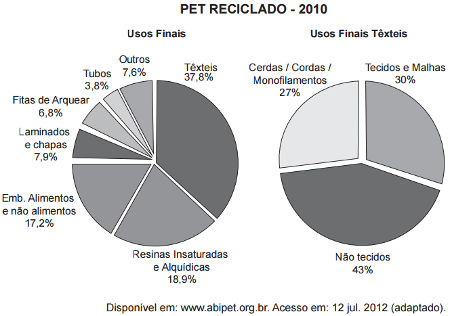
De acordo com os gráficos, a quantidade de embalagens PET recicladas destinadas à produção de tecidos e malhas, em kton, é mais aproximada de
a) 16,0
b) 22,9
c) 32,0
d) 84,6
e) 106,6
Solução
Observe que a porcentagem destinada a tecidos e malhas é 30% dos usos finais têxteis, que, por sua vez, é uma porcentagem de 37,8% de todos os usos finais. Sendo assim, precisaremos calcular 30% de 37,8% de 282 kton. Esse cálculo pode ser expresso por multiplicações da seguinte maneira:
30%·37,8%·282
Para resolver essa questão, lembre-se de que uma porcentagem é uma fração de denominador 100. Logo, podemos transformar a multiplicação acima na multiplicação de frações a seguir:
30 · 37,8·282
100 100
Conforme as regras de multiplicação de frações dadas no início do texto, basta multiplicar numeradores por numeradores e denominadores por denominadores. A única observação é a de que o denominador de 282 é 1.
30 · 37,8·282 = 319788
100 100 10000
Dividindo numerador por denominador, pois toda fração representa uma divisão, teremos:
319788 = 31,9788
10000
Esse valor é aproximadamente 32 kton.
Gabarito: letra C.
(Enem 2015) – A expressão “Fórmula de Young” é utilizada para calcular a dose infantil de um medicamento, dada a dose do adulto:
Dose de criança = Idade da criança (em anos) · dose de adulto
Idade da criança (em anos) + 12
Uma enfermeira deve administrar um medicamento X a uma criança inconsciente, cuja dosagem de adulto é de 60 mg. A enfermeira não consegue descobrir onde está registrada a idade da criança no prontuário, mas identifica que, algumas horas antes, foi administrada a ela uma dose de 14 mg do medicamento Y, cuja dosagem de adulto é 42 mg. Sabe-se que a dose da medicação Y administrada à criança estava correta.
Então, a enfermeira deverá ministrar uma dosagem do medicamento X, em miligramas, igual a
a) 15
b) 20
c) 30
d) 36
e) 40
Solução
Esse exercício envolverá uma multiplicação de frações, mas, antes, é preciso resolver equações. Para resolvê-lo, mudaremos a fórmula para facilitar a organização dos cálculos, portanto, C = dose da criança, i = Idade da criança e A = Dose do adulto.
C = i · A
i + 12
Substituindo os valores conhecidos para o medicamento Y, teremos:
14 = i · 42
i + 12
Resolvendo a equação, teremos:
(i + 12)14 = i· 42
14i + 168 = 42i
42i – 14i = 168
28i = 168
i = 168
28
i = 6
Sabendo que a idade da criança é 6 anos, temos que:
C = 6 · 60
6 + 12
C = 6 · 60
18
Observe que é necessário multiplicar uma fração por um número inteiro. Como todo número inteiro é uma fração de denominador 1, teremos:
C = 6 · 60 = 360
18 1 18
Dividindo numerador por denominador, encontraremos 20 mg como dosagem do medicamento X.
Gabarito: letra B.