Olá, pessoal! A prova do Enem está cada vez mais perto, e se você quer se dar bem em Matemática e suas Tecnologias, não pode ter nenhuma dúvida sobre funções, hein!? Em todos os anos sempre encontramos questões sobre funções, que podem apresentar-se através de gráficos e tabelas, em meio a problemas ou mesmo apenas com a lei de formação da função.
Cada tipo de função possui suas características principais, e é importante ter conhecimento sobre cada uma delas. Hoje vamos discutir sobre os dois tipos mais comuns: a função do 1° grau e a função do 2° grau. Veja um comparativo entre essas funções:
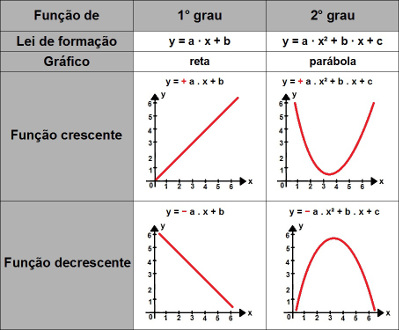
Principais características das funções de 1° e 2° grau
Vejamos como se apresentaram algumas questões sobre funções em exames anteriores do Enem:
Questão sobre Funções no Enem de 2011
Uma empresa de telefonia fixa oferece dois planos aos seus clientes: no plano K, o cliente paga R$ 29,90 por 200 minutos mensais e R$ 0,20 por cada minuto excedente; no plano Z, paga R$ 49,90 por 300 minutos mensais e R$ 0,10 por cada minuto excedente.
O gráfico que representa o valor pago, em reais, nos dois planos em função dos minutos utilizados é:
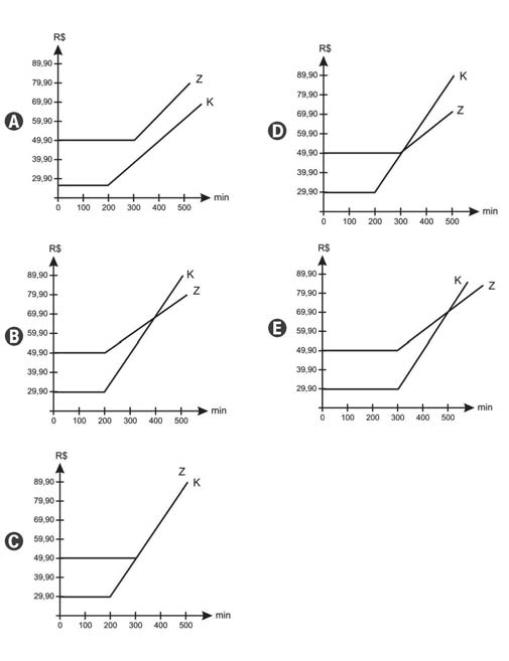
Alternativas da questão
Resolução:
Para compreender os dois planos oferecidos pela empresa de telefonia, vamos verificar qual é a lei da função que rege cada oferta. Considere x como o tempo em minutos.
Plano K: R$ 29,90 por 200 minutos mensais e R$ 0,20 por cada minuto excedente;
Plano Z: R$ 49,90 por 300 minutos mensais e R$ 0,10 por cada minuto excedente.
Podemos afirmar que, para x ≤ 200, o gráfico da função k(x) é uma constante, tal que k(x) = 29,90. O mesmo ocorre para a função z(x): para x ≤ 300, o gráfico da função é uma constante, tal que z(x) = 49,90. A partir dessas duas situações, ambas as funções tornam-se crescentes.
Por exemplo, se o consumidor do plano K utilizar 201 minutos, o valor de sua conta aumentará, pois ele excedeu em 1 minuto o tempo permitido, portanto, ele pagará k(201) = 29,90 + 0,20·(201 – 200) = 29,90 + 0,20 · 1 = 30,10.
Agora que compreendemos o funcionamento de k(x) e de z(x), vamos verificar se em algum momento as funções interceptam-se, isto é, se existe algum valor de x tal que k(x) = z(x):
k(x) = z(x)
29,90 + 0,20·(x – 200) = 49,90 + 0,10·(x – 300)
29,90 + 0,20·x – 40 = 49,90 + 0,10·x – 30
0,20·x – 10,10 = 19,90 + 0,10·x
0,20·x – 0,10·x = 19,90 + 10,10
0,10·x = 30,00
x = 30,00
0,10
x = 300
Os gráficos de k(x) e de z(x) interceptam-se quando x = 300 e k(x) = z(x) = 49,90. Esse é o único ponto em que ambas as funções possuem os mesmos valores. Para todos os demais valores de x, as funções são distintas. Observando as alternativas, o único gráfico que corresponde à análise feita é o que está representado na letra d, portanto, essa é a alternativa correta.
Questão sobre Funções no Enem de 2010
As sacolas plásticas sujam florestas, rios e oceanos e quase sempre acabam matando por asfixia peixes, baleias e outros animais aquáticos. No Brasil, em 2007, foram consumidas 18 bilhões de sacolas plásticas. Os supermercados brasileiros se preparam para acabar com as sacolas plásticas até 2016. Observe o gráfico a seguir, em que se considera a origem como o ano de 2007.

Gráfico da questão do Enem de 2010
De acordo com as informações, quantos bilhões de sacolas plásticas serão consumidos em 2011?
a) 4,0.
b) 6,5.
c) 7,0.
d) 8,0.
e) 10,0.
Resolução:
De acordo com o enunciado do exercício, a origem do eixo x é o ano de 2007, e o próximo ano destacado corresponde a 9 anos após 2007, portanto, o ano de 2016.
Após uma cuidadosa análise do gráfico da função, podemos identificar dois pontos: (0, 18) e (9, 0). Através desses pontos, vamos encontrar a lei de formação da função. Como o gráfico é uma reta, sabemos que essa é uma função do 1° grau, portanto, do tipo y = a · x + b. Dessa forma, vamos substituir os pontos (0, 18) e (9, 0) nessa equação:
y = a · x + b
| (0, 18) → 18 = a . 0 + b b = 18 |
(9, 0) → 0 = a . 9 + 18 – 9 . a = 18 a = – 2 |
Podemos afirmar que a lei de formação da função representada no gráfico é dada por:
y = – 2 · x + 18,
*y é o número de sacolas e x é o ano (subtraindo 2007 de x).
Para que não haja confusão a respeito do valor de x, podemos reescrever a função da seguinte forma:
y = – 2 · (x – 2007) + 18
Agora que temos a lei de formação da função, podemos determinar quantos bilhões de sacolas plásticas serão consumidos quando tivermos x = 2011:
y = – 2 · (x – 2007) + 18
y = – 2 · (2011 – 2007) + 18
y = – 2 · 4 + 18
y = – 8 + 18
y = 10
Portanto, em 2011, serão produzidos 10 bilhões de sacolas. A alternativa correta é a letra e.
Bons estudos!







