Olá, pessoal! Vocês já observaram a quantidade de questões envolvendo porcentagem nas provas de Matemática e suas Tecnologias do Enem? A cada ano podemos encontrar várias questões que cobram conhecimento nessa área da Matemática Financeira. Se você ainda tem dúvidas sobre o assunto, fique tranquilo, pois vamos solucioná-las para você!
Primeiramente vamos lembrar o que é porcentagem:
Porcentagem é uma razão entre dois números com base 100. Seu símbolo principal é %.
Podemos representar uma porcentagem ou uma taxa percentual de três maneiras distintas, sem qualquer perda de valor. Por exemplo, dada a porcentagem 10%, podemos realizar sua leitura como 10 porcento, o que equivale a 10 por cem ou à fração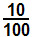 
, que, por sua vez, é equivalente a 0,1, pois, dividindo o numerador pelo denominador, encontramos o quociente 0,1. Em resumo, podemos afirmar que:
10% = 10 = 0,1
100
Analogamente, temos outros exemplos de porcentagens:
50% = 50 = 0,5
100
22% = 22 = 0,22
100
3% = 3 = 0,03
100
0,5% = 0,5 = 0,005
100
Vejamos a resolução de algumas questões do Enem de anos anteriores para conferir como elas costumam cobrar porcentagem ou taxa percentual.
Questão com porcentagem no Enem de 2011
O Índice de Massa Corporal (IMC) é largamente utilizado há cerca de 200 anos, mas esse cálculo representa muito mais a corpulência que a adiposidade, uma vez que indivíduos musculosos e obesos podem apresentar o mesmo IMC. Uma nova pesquisa aponta o Índice de Adiposidade Corporal (IAC) como uma alternativa mais fidedigna para quantificar a gordura corporal, utilizando a medida do quadril e a altura. A figura mostra como calcular essas medidas, sabendo-se que, em mulheres, a adiposidade normal está entre 19% e 26%.
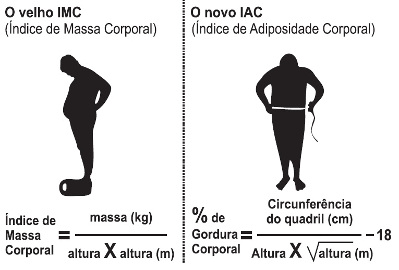
Questão com probabilidade no Enem de 2011
Disponível em: http://www1.folha.uol.com.br. Acesso em: 24 abr. 2011(adaptado).
Uma jovem com IMC = 20 kg/m², 100 cm de circunferência dos quadris e 60 kg de massa corpórea resolveu averiguar seu IAC. Para se enquadrar aos níveis de normalidade de gordura corporal, a atitude adequada que essa jovem deve ter diante da nova medida é:
(Use √3 = 1,7 e √1,7 = 1,3)
a) reduzir seu excesso de gordura em cerca de 1%.
b) reduzir seu excesso de gordura em cerca de 27%.
c) manter seus níveis atuais de gordura.
d) aumentar seu nível de gordura em cerca de 1%.
e) aumentar seu nível de gordura em cerca de 27%.
Resolução:
Para calcular o IAC da jovem, precisamos conhecer sua altura (h). Dessa forma, vamos utilizar a fórmula do cálculo do IMC:
IMC = massa
h . h
20 = 60
h²
h² = 60
20
h² = 3
h = √3
h = 1,7
Seja x a porcentagem de gordura corporal da jovem, vamos determiná-la através da fórmula do IAC:
x = circunferência do quadril – 18
h . √h
x = 100 – 18
1,7 . √1,7
x = 100 – 18
1,7 . 1,3
x = 100 – 18
2,21
x = 45,25 – 18
x = 27,25
O índice de adiposidade da jovem é de 27,25%, mas de acordo com o enunciado, o adequado deve estar entre 19% e 26%. Temos então que:
27,25% – 26% = 1,25%
Isso implica que o IAC da jovem deve diminuir cerca de 1,25% para que se adeque ao indicado. Portanto, a alternativa correta é a letra a.
Questão com porcentagem no Enem de 2011
Para aumentar as vendas no início do ano, uma loja de departamentos remarcou os preços de seus produtos 20% abaixo do preço original. Quando chegam ao caixa, os clientes que possuem o cartão fidelidade da loja têm direito a um desconto adicional de 10% sobre o valor total de suas compras.
Um cliente deseja comprar um produto que custava R$ 50,00 antes da remarcação de preços. Ele não possui o cartão fidelidade da loja.
Caso esse cliente possuísse o cartão fidelidade da loja, a economia adicional que obteria ao efetuar a compra, em reais, seria de
a) 15,00.
b) 14,00.
c) 10,00.
d) 5,00.
e) 4,00.
Resolução:
Como o cliente não possui o cartão fidelidade da loja, o produto que ele comprará receberá apenas o desconto promocional de 20%. Para descobrir qual será o novo preço do produto que, originalmente, custava R$ 50, utilizaremos uma regra de três:
100% = R$ 50,00
20% = x
100.x = 20 . 50
100 x = 1000
x = 1000
100
x = 10 reais
O produto recebeu um desconto de R$ 10. Se antes ele custava R$ 50, na promoção, custará R$ 40.
Se o cliente possuísse o cartão fidelidade da loja, o preço promocional de R$ 40 receberia ainda um abatimento de 10%. Vamos utilizar uma regra de três novamente para verificar o valor do novo desconto:
100% = R$ 40,00
10% = x
100.x = 10 . 40
100 x = 400
x = 400
100
x = 4 reais
Se o cliente obtivesse o cartão fidelidade, poderia alcançar um novo desconto de R$ 4. Portanto, a alternativa correta é a letra e.
Se você deseja aprender um pouco mais sobre porcentagem, confira os exercícios que selecionamos para você: Exercícios sobre Porcentagem, Exercícios sobre a História das Porcentagens e Exercícios sobre Porcentagem utilizando Regra de Três.
Bons estudos!
