Olá, galera! Vocês já observaram a quantidade de questões envolvendo equações na prova de Matemática e suas Tecnologias do Enem? As equações estão sempre presentes, sejam elas do 1°, do 2° ou de outro grau, o certo é que você vai encontrá-las em várias questões! Que tal então relembrar esses dois tipos de equações?
As equações do 1° grau podem aparecer explícitas, envolvidas em algum problema ou em meio a tabelas e gráficos. Mas independentemente de como elas vierem, a forma de resolvê-las não varia muito. Em geral, a equação de 1° grau é do tipo ax + b = 0, em que a e b são os coeficientes da equação (a ≠ 0), e x é a variável. Uma equação do 1° grau pode ter apenas uma solução ou nenhuma.
As equações do 2° grau também podem aparecer de diversas formas, mas sempre obedecerão a um mesmo padrão: ax² + bx + c = 0 (a, b e c são os coeficientes da equação (a ≠ 0), e x é a variável). Uma equação do 2° grau pode ter duas soluções, uma ou nenhuma.
Existem formas alternativas para resolver uma equação do 2° grau incompleta, mas, em geral, podemos sempre utilizar a fórmula de Bhaskara ao nos depararmos com equações do 2° grau. Utilizando Bhaskara, basta substituir os coeficientes na seguinte equação:
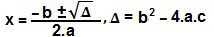
Em sua prova, podem ainda aparecer questões que envolvam equações de 3° grau, de 4° grau (biquadradas) e outras. O ideal é que você procure aproximá-las de uma equação de 2° grau para facilitar seu desenvolvimento.
Vamos ver a resolução comentada de questões anteriores do Enem que apresentaram equações:
Questão com Equações no Enem de 2010
Desde 2005, o Banco Central não fabrica mais a nota de R$ 1,00 e, desde então, só produz dinheiro nesse valor em moedas. Apesar de ser mais caro produzir uma moeda, a durabilidade do metal é 30 vezes maior que a do papel. Fabricar uma moeda de R$ 1,00 custa R$ 0,26, enquanto uma nota custa R$ 0,17, entretanto, a cédula dura de oito a onze meses.
Disponível em: http://noticias.r7.com. Acesso em: 26 abr. 2010.
Com R$ 1 000,00 destinados a fabricar moedas, o Banco Central conseguiria fabricar, aproximadamente, quantas cédulas a mais?
a) 1 667.
b) 2 036.
c) 3 846.
d) 4 300.
e) 5 882.
Resolução:
De acordo com o texto, gasta-se R$ 0, 26 para produzir uma moeda de um real e apenas R$ 0,17 para produzir uma nota de mesmo valor. Para saber quantas moedas ou cédulas podem ser produzidas com determinado valor, basta fazer o quociente entre o valor empregado e o custo da moeda ou da cédula. Claramente podemos ver que, com um mesmo investimento, podem ser produzidas mais cédulas do que moedas.
Para determinar quantas cédulas seriam produzidas a mais (x), vamos determinar a diferença entre o quociente das cédulas e das moedas. De forma simplificada, temos a seguinte equação:
x = valor empregado – valor empregado
custo por cédula custo por moeda
O enunciado informa que o valor empregado é de R$ 1 000,00. Já sabemos que o custo por moeda é de R$ 0,26 e por cédula é de R$ 0,17. Sendo assim, temos:
x = 1 000 – 1 000
0,17 0,26
x ≈ 5 882,34 – 3 846,14
x ≈ 2 036,2
Portanto, com R$ 1 000,00, podem ser produzidas cerca de 2 036 cédulas a mais do que moedas de um real. A alternativa que indica a resposta correta é a letra b.
Questão com Equações no Enem de 2010
Um laticínio possui dois reservatórios de leite. Cada reservatório é abastecido por uma torneira acoplada a um tanque resfriado. O volume, em litros, desses reservatórios depende da quantidade inicial de leite no reservatório e do tempo t, em horas, em que as duas torneiras ficam abertas. Os volumes dos reservatórios são dados pelas funções V1(t) = 250t³ - 100t + 3000 e V2(t) = 150t³ + 69t + 3000.
Depois de aberta cada torneira, o volume de leite de um reservatório é igual ao do outro no instante t = 0 e, também, no tempo t igual a
a) 1,3 h.
b) 1,69 h.
c) 10,0 h.
d) 13,0 h.
e) 16,9 h.
Resolução:
Para descobrir em qual momento será igual o volume de leite nos dois reservatórios, basta igualar V1(t) e V2(t). Sendo assim, temos:
250t³ – 100t + 3000 = 150t³ + 69t + 3000
250t³ – 100t = 150t³ + 69t + 3000 – 3000
250t³ – 100t = 150t³ + 69t
Temos aqui uma equação do 3° grau, pois o maior índice da variável t é 3. Como dissemos anteriormente, o ideal é tentar transformar essa igualdade em uma equação do 2° grau. Para tanto, observe que todos os termos estão acompanhados de t. Podemos então dividir toda a equação por t:
250t³ – 100t = 150t³ + 69t
t t t t
250t² – 100 = 150t²+ 69
250t² – 150t² – 100 – 69 = 0
100t² – 169 = 0
Podemos resolver essa equação do 2° grau de duas formas diferentes. Primeiramente vamos utilizar a fórmula de Bhaskara, lembrando que a = 100, b = 0 e c = – 169:
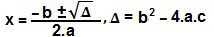
∆ = b² – 4.a.c
∆ = 0² – 4.100.(– 169)
∆ = 67600
t = – b ± √∆
2.a
t = – 0 ± √67600
2.100
t = ± 260
200
t1 = 260 = 1,3
200
t2 = – 260 = – 1,3
200
Como estamos falando de tempo, podemos descartar o resultado negativo. Sendo assim, t1 = 1,3 h. Portanto, a resposta correta é a letra a.
Vamos resolver essa equação incompleta do 2° grau de uma forma alternativa, sem utilizar a fórmula de Bhaskara:
100t² – 169 = 0
100t² = 169
t² = 169
100
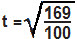
t = √169
√100
t = 13
10
t = 1,3
Observe que obtivemos o mesmo resultado, logo, como dito anteriormente, não há uma única forma de resolver uma equação do 2° grau.
Se você deseja aprender um pouco mais sobre equações, confira os exercícios que selecionamos para você:
- Equação do 1º grau com Duas Incógnitas;
- Equação do 1º Grau com uma Incógnita;
- Problemas Envolvendo o Uso de Equações;
- Exercícios sobre Equações e os problemas matemáticos.
Bons estudos!







