Estatística é uma área da Matemática que se ocupa da coleta, organização e análise de dados. Os dados podem ser quantitativos ou qualitativos e a organização deles é feita por meio de tabelas e gráficos. Já a análise dos dados nos níveis mais básicos da Estatística é feita por meio de medidas de centralidade (moda, média e mediana), observações de gráficos e tabelas, porcentagens e também proporcionalidade.
Esse conteúdo é amplamente explorado nas questões do Enem, que também tem o objetivo de avaliar a leitura, análise e interpretação de dados. Para uma melhor compreensão, tomaremos como exemplos alguns exercícios do Enem para discutir alguns desses conceitos.
Tabelas
O exercício abaixo será resolvido e comentado para discutirmos uma das formas de organizar dados em uma tabela. Observe que a primeira linha é usada para colocar o título da tabela. A segunda linha e primeira coluna contêm indicações do modo como a tabela é preenchida e/ou as variáveis em questão. Os dados em si são colocados nas demais linhas e colunas.
Observe o exemplo:
(ENEM – 2009) Os planos de controle e erradicação de doenças em animais envolvem ações de profilaxia e dependem em grande medida da correta utilização e interpretação de testes diagnósticos. O quadro abaixo mostra um exemplo hipotético de aplicação de um teste diagnóstico

Considerando que, no teste diagnostico, a sensibilidade é a probabilidade de um animal infectado ser classificado como positivo e a especificidade é a probabilidade de um animal não ser infectado e ter resultado negativo, a interpretação do quadro permite inferir que
a) A especificidade aponta um número de 5 falsos positivos.
b) O teste, a cada 100 indivíduos infectados, classificaria 90 como positivos.
c) O teste classificaria 96 como positivos em cada 100 indivíduos não infectados.
d) Ações de profilaxia são medidas adotadas para o tratamento de falsos positivos.
e) Testes de alta sensibilidade resultam em maior número de falsos negativos comparado a um teste de baixa sensibilidade.
Solução:
Não existe outra maneira de solucionar esse exercício do que procurar os dados que comprovem ou refutem as alternativas na tabela e no texto ao redor dela. ATENÇÃO: o texto que o exercício traz é tão importante quanto os dados da tabela. Prova disso é a alternativa A, pois a especificidade é definida no texto, e não na tabela, como a probabilidade de um animal não ser infectado e ter um resultado negativo. Observando a tabela, a especificidade é de 912 animais. Portanto, a alternativa está incorreta.
A alternativa correta é a letra B. Para verificar isso, observe que o texto da alternativa menciona apenas o número de indivíduos infectados. Há uma coluna somente para isso na tabela. São 45 indivíduos com teste positivo para cada 50 infectados. Por regra de 3, a cada 100 infectados, 90 terão resultado positivo no teste.
Gráficos
Os dados também podem vir organizados na forma de gráficos, e essas representações são mais frequentes no Enem. Observe o exemplo a seguir:
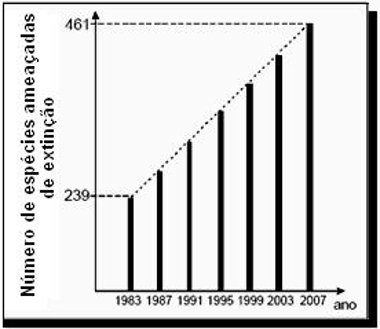
(ENEM) O gráfico, obtido a partir de dados do Ministério do Meio Ambiente, mostra o crescimento do número de espécies da fauna brasileira ameaçadas de extinção.
Se mantida, pelos próximos anos, a tendência de crescimento mostrada no gráfico, o número de espécies ameaçadas de extinção em 2011 será igual a:
a) 465
b) 493
c) 498
d) 538
e) 699
Observe que o título do gráfico não aparece em sua parte superior, mas do lado esquerdo. O importante é que, assim como na tabela, expresse a informação necessária para compreensão dos dados. Esse gráfico é conhecido como gráfico de colunas, pois cada quantidade é expressa por meio de uma barra vertical.
Solução:
Observe que o crescimento do número de espécies ameaçadas de extinção é linear e está demarcado em períodos de quatro anos no gráfico. A pergunta é exatamente para o fim de mais um período de quatro anos, logo, basta descobrir o aumento do número de animais em cada período de quatro anos e somar esse acréscimo a 461.
Para tanto, usaremos conhecimentos de progressão aritmética, mais especificamente a fórmula para encontrar um termo qualquer. Se 239 for o primeiro e 461 for o último (sétimo), basta encontrar a razão para saber o aumento em um período de quatro anos. Observe:
a7 = a1 + (n – 1)r
461 = 239 + (7 – 1)r
461 – 239 = 6r
222 = 6r
r = 222
6
r = 37
Assim, em 2011, o número de espécies ameaçadas de extinção será:
461 + 37 = 498
Gabarito: Letra C
Medidas de centralidade
Todas as informações de gráficos e tabelas possuem algum elemento que pode servir para representar todos os outros. Esse elemento é conhecido como medida de centralidade. As medidas mais importantes para a estatística básica são:
-
Moda: Entre todos os dados de uma lista, tabela ou gráfico, existe um que é mais frequente. Esse dado é chamado de moda. Para encontrá-la, encontre o dado que mais aparece em uma lista e ele será a moda. Existem, é claro, listas que possuem duas ou mais modas;
-
Mediana: Escrevendo em ordem crescente os dados de uma lista, tabela ou gráfico, a mediana é o valor que fica exatamente no meio de todos os outros. Se a lista tiver um número par de dados, não existirá um valor que ficará exatamente no centro, então, basta fazer a média aritmética dos dois valores centrais;
-
Média aritmética: é a soma de todos os dados dividida pela quantidade de dados que foram somados. A média aritmética também pode levar pesos em consideração. Isso acontece quando um valor possui mais importância e acaba sendo multiplicado por um número que recebe o nome de peso. Nas universidades, por exemplo, é comum que as primeiras provas tenham pesos menores que as últimas na média final do aluno. Na média aritmética ponderada, é feito algo parecido com a média simples: somam-se todos os valores multiplicados pelos seus respectivos pesos e divide-se o resultado pela soma dos pesos.
(ENEM 2010) O quadro seguinte mostra o desempenho de um time de futebol no último campeonato. A coluna da esquerda mostra o número de gols marcados e a coluna da direita informa em quantos jogos o time marcou aquele número de gols.
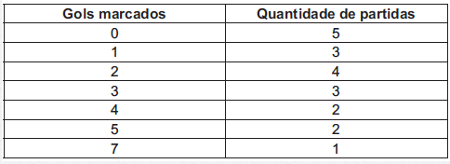
Se X, Y e Z são, respectivamente, a média, a mediana e a moda dessa distribuição, então
A) X = Y < Z.
B) Z < X = Y.
C) Y < Z < X.
D) Z < X < Y.
E) Z < Y < X.
Solução:
Observe primeiramente que a moda é zero, pois foi o número de gols marcado no maior número de partidas.
As quantidades de gols devem ser colocadas em ordem crescente para encontrar a mediana:
0, 0, 0, 0, 0, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 4, 4, 5, 5, 7
Observe que existem dois valores centrais. Portanto, a mediana será:
2 + 2 = 4 = 2
2 2
Já a média pode ser obtida pela técnica de média ponderada ou de média simples. Para tanto, basta somar os elementos da lista acima e dividir o resultado por 20 ou, como média ponderada, considerar o número de partidas como peso. Ambos os cálculos darão o mesmo resultado.
0 + 0 + 0 + 0 + 0 + 1 + 1 + 1 + 2 + 2 + 2 + 2 + 3 + 3 + 3 + 4 + 4 + 5 + 5 + 7 =
20
45 = 2,25
20
Sabendo que a média é X = 2,25, a mediana é Y = 2 e a moda é Z = 0, teremos:
X > Y > Z ou Z < Y < X
Gabarito: letra E.







