Olá, candidato! Você sabia que grandezas proporcionais são cobradas na prova de Matemática e suas Tecnologias do Enem? Mas pode ficar tranquilo porque, ao fim deste texto, não lhe restará dúvidas para lidar com proporções, principalmente se elas estiverem em sua prova do Enem!
Primeiramente, você se lembra da definição de proporção? Todas as proporções são igualdades estabelecidas entre razões, isto é, se temos duas razões iguais, podemos afirmar que elas formam uma proporção. O quociente entre 1 e 2, por exemplo, resulta em 0,5, assim como a divisão entre 3 e 6. Podemos afirmar que a igualdade a seguir é uma proporção:
1 = 3
2 6
Podemos ainda efetuar uma multiplicação cruzada entre os elementos dessa proporção sem perder o efeito da igualdade, isto é:
1 = 3 ↔ 2 · 3 = 1 · 6
2 6
De modo geral, se duas razões a/b e c/d são equivalentes, podemos dizer que vale a proporção:
a = c
b d
A multiplicação cruzada que fizemos anteriormente é garantida pela propriedade fundamental das proporções, que garante que o produto dos extremos (a e d) sempre é igual ao produto dos meios (b e c):
a = c ↔ a · d = b · c
b d
Confira agora a resolução comentada de algumas questões sobre proporção em provas anteriores do Enem:
Questão com Proporção no Enem de 2012
José, Carlos e Paulo devem transportar em suas bicicletas uma certa quantidade de laranjas. Decidiram dividir o trajeto a ser percorrido em duas partes, sendo que ao final da primeira parte eles redistribuiriam a quantidade de laranjas que cada um carregava dependendo do cansaço de cada um. Na primeira parte do trajeto José, Carlos e Paulo dividiram as laranjas na proporção 6 : 5 : 4, respectivamente. Na segunda parte do trajeto José, Carlos e Paulo dividiram as laranjas na proporção 4 : 4 : 2, respectivamente.
Sabendo-se que um deles levou 50 laranjas a mais no segundo trajeto, qual a quantidade de laranjas que José, Carlos e Paulo, nessa ordem, transportaram na segunda parte do trajeto?
a) 600, 550, 350
b) 300, 300, 150
c) 300, 250, 200
d) 200, 200, 100
e) 100, 100, 50
Resolução:
Para estabelecer um parâmetro de comparação nas duas situações, vamos expressar por meio de frações a quantidade de laranjas carregada por cada um. Se somarmos os valores da proporção que se referem ao primeiro momento, obteremos 6 + 5 + 4 = 15. Dessa forma, podemos afirmar que as quantidades inicialmente transportadas são valores proporcionais a:
José = 6
15
Carlos = 5
15
Paulo = 4
15
Da mesma forma, pela proporção do segundo momento, temos 4 + 4 + 2 = 10. Podemos novamente afirmar que a quantidade de laranjas carregadas é agora proporcional a:
José = 4
10
Carlos = 4
10
Paulo = 2
10
Todavia, apenas por essas proporções, não é tão simples verificar quem carregou mais laranjas em cada momento. Para facilitar essa visualização, vamos deixar todas as frações com um mesmo denominador. Através da fatoração, é fácil ver que o mínimo múltiplo comum entre 10 e 15 é 30. As proporções podem ser reescritas novamente da seguinte forma:
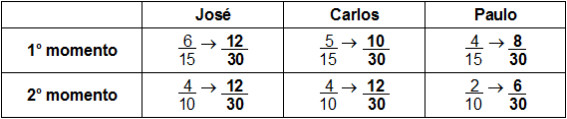
Podemo ver mais claramente que José manteve a quantidade de laranjas que estava carregando inicialmente e que Paulo diminuiu a sua carga. Já Carlos aumentou a quantidade que estava transportando. Logo, quem levou 50 laranjas a mais no segundo trajeto foi Carlos.
Considere que x seja a quantidade total de laranjas que os rapazes carregaram. Se Carlos carregava dez trinta avos do total de laranjas e, ao acrescentar 50 laranjas, passou a transportar doze trinta avos do total, chegamos à seguinte equação:
10 . x + 50 = 12 . x
30 30
10.x + 1500 = 12.x
30 30
1500 = 12.x – 10.x
1500 = 2.x
2.x = 1500
x = 1500
2
x = 750
O total transportado era de 750 laranjas. Mas se no segundo momento José e Carlos levaram 4/10 do total cada um e Paulo levou 2/10 do total, temos:
José
4 . 750 = 4 . 75 = 300
10
Carlos
4 . 750 = 4 . 75 = 300
10
Paulo
2 . 750 = 2 . 75 = 150
10
Portanto, a resposta correta é a letra b, que indica que José, Carlos e Paulo levaram, respectivamente, 300, 300 e 200 laranjas cada um.
Questão com Proporção no Enem de 2011
Nos últimos cinco anos, 32 mil mulheres de 20 a 24 anos foram internadas nos hospitais do SUS por causa de AVC. Entre os homens da mesma faixa etária, houve 28 mil internações pelo mesmo motivo.
Época. 26 abr. 2010 (adaptado)
Suponha que, nos próximos cinco anos, haja um acréscimo de 8 mil internações de mulheres e que o acréscimo de internações de homens por AVC ocorra na mesma proporção.
De acordo com as informações dadas, o número de homens que seriam internados por AVC, nos próximos cinco anos, corresponderia a
a) 4 mil.
b) 9 mil.
c) 21 mil.
d) 35 mil.
e) 39 mil.
Resolução:
De acordo com o enunciado, em cinco anos, houve um total de 32.000 mulheres internadas. Se aumentarem 8.000 mulheres nos próximos cinco anos, teremos a seguinte proporção:
8000 = 8 = 1
32000 32 4
A proporção de ¼ corresponde a 0,25, também equivalente a 25%. Se a quantidade de homens internados, que foi de 28.000, aumentar nessa mesma proporção, teremos:
1 . 28000 = 28000 = 7000
4 4
Aumentando 7.000 homens aos 28.000 registrados anteriormente, teremos um total de 35.000 homens internados por AVC nos próximos cinco anos. Logo, a alternativa que indica a resposta correta é a letra d.
Bons estudos!








